Networkbridge NBO

Primzahlen Unsiverum: Riemannsche Vermutung 1859

Neue Mustererkennung durch alternative Zahlensysteme und systematische Darstellung

Inhalt

1. Enführung Primzahlen sichtbar gemacht
2. Beobachtete Regelmäßigkeiten / Muster
3. Verwendete drei Software-Werkzeuge
4. Software 1 - Dezimales Zahlensystem Basis 10
5. Software 2 - Frei wählbare Variable Basis
6. Software 3 - Große Zahlensysteme (über Basis 36 hinaus)
7. Eigene Experimente - Schritt für Schritt
8. Zielsetzung
9. Beispiele Primzahlen Tabellen durch Software 1 - 3
10. RGUMS Prime Numbers Software 1 - 3 / markieren / kopieren

1. Einführung: Primzahlen sichtbar gemacht

Primzahlen gelten seit Jahrhunderten als geheimnisvoll. Sie sind eindeutig definiert – und dennoch schwer vorherzusagen. Trotz intensiver Forschung hat sich seit der Veröffentlichung der Riemannschen Vermutung im Jahr 1859 unser grundlegendes Verständnis über ihre innere Struktur kaum verändert.
Diese Seite geht einen anderen Weg. Statt neue Theorien aufzustellen, macht sie Primzahlen sichtbar - in Tabellen, die so aufgebaut sind, dass Muster nicht berechnet, sondern gesehen werden können.

2. Beobachtete Regelmäßigkeiten / Muster

Bei der Darstellung großer Primzahlbereiche in Tabellen unter mithilfe der unten aufgeführten Software Werkzeuge, zeigen sich wiederkehrende Strukturen: Im Dezimalsystem treten sogenannte Zweier-Blöcke auf – zwei Primzahlen untereinander. Mehr als zwei direkt aufeinanderfolgende Primzahlen erscheinen so jedoch nie. In einem Zahlensystem mit 42 Ziffern entstehen entsprechend Vierer-Blöcke, aber ebenfalls niemals größere. In Basen wie 9 oder 11 treten solche Zweier-Blöcke überhaupt nicht auf. Zahlenendungen wie 2, 4, 5, 6, 8 und 0, die im Dezimalsystem (Basis 10) bei Primzahlen nicht vorkommen, verhalten sich in anderen Zahlensystemen anders.

3. Verwendete 3 Software-Werkzeuge

Zur Reproduktion und Erweiterung dieser Beobachtungen stehen drei einfache Software-Varianten zur Verfügung. Alle arbeiten mit derselben Primzahldefinition, unterscheiden sich jedoch in der zugrunde gelegten Darstellung. Sie sind bewusst so gestaltet, dass keine mathematischen Vorkenntnisse nötig sind.

4. RGUMS Prime Numbers Software 1 – Dezimales Zahlensystem Basis 10

Es muss nur der Bereich der Primzahlen Tabelle eingegeben werden. Ein Doppelklick auf die erzeugte Datei öffnet sie sofort in ihrem Browser.

<title>Primzahlen-Tabelle (1–1000)</title> Wert ändern (1-1000)
let zahl = 1; Wert ändern = 1;
for (let zeile = 0; zeile < 100; zeile++) { Wert ändern < 100;

5. RGUMS Prime Numbers Software 2 – Frei wählbare Variable Basis

Das Dezimalsystem ist keine Notwendigkeit – es ist eine Gewohnheit. Wir nutzen zehn Ziffern, weil wir zehn Finger haben. Mit acht oder zwölf Fingern hätten wir andere Zahlensysteme entwickelt. In dieser Software kannst du die Basis selbst festlegen, zum Beispiel hier die 16.

:const BASE = 16; Wert ändern 16;

Die Primzahl-Logik bleibt gültig – aber die sichtbaren Muster verändern sich deutlich, wie die beigefügten PDF-Beispiele zeigen.

6. RGUMS Prime Numbers Software 3 – Große Zahlensysteme (über Basis 36 hinaus)

Diese Version ist speziell dafür entwickelt, auch sehr große Basen darzustellen. Hier sind drei Werte wichtig die vorher bestimmt werden sollten, zum Beispiel die 42 BASE / 42 COLS und die für diesen Fall die 42 Zeichen DIGITS:

const BASE = 42; Wert ändern 42;
const START = 1; Wert ändern 1;
const ROWS = 100; // 100 x 42 = 4200 Zahlen Werte ändern 100; // 100 x 42 = 4200
const COLS = 42; Wert ändern 42;
const DIGITS = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdef";

BASE bestimmt das Zahlensystem
COLS bestimmt die Spaltenzahl der Tabelle
DIGITS legt fest, welche Zeichen als Ziffern verwendet werden

Wenn du eine Basis größer als 42 verwenden möchtest, kannst du einfach weitere Kleinbuchstaben an die DIGITS-Zeile anhängen.

7. Eigene Experimente – Schritt für Schritt

Öffne einen Texteditor
Einfügen des vorher kopierten RGUMS Prime Numbers Software html-code.
Zahlen / Werte ändern
Wähle Datei → Speichern unter
Lege den Speicherort fest (z. B. Schreibtisch)
Gib einen Dateinamen ein und ergänze ihn am Einde mit .html
Stelle sicher, dass „Alle Dateien“ ausgewählt ist
Speichern
Ein Doppelklick auf die erzeugte Datei öffnet sie sofort in ihrem Browser.

8. Zielsetzung

Die bereitgestellten Tabellen und PDF-Dokumente dienen als Anschauungsmaterial. Sie sollen dazu anregen, bekannte Eigenschaften von Primzahlen in unterschiedlichen Darstellungssystemen zu vergleichen und weitere Muster zu identifizieren. Der Ansatz ist bewusst offen und explorativ. Er richtet sich sowohl an mathematisch geschulte Leser als auch an interessierte Beobachter ohne formale Ausbildung, da alle relevanten Strukturen unmittelbar visuell zugänglich sind.

9a. Beispiele Primzahlen Tabellen Software 1

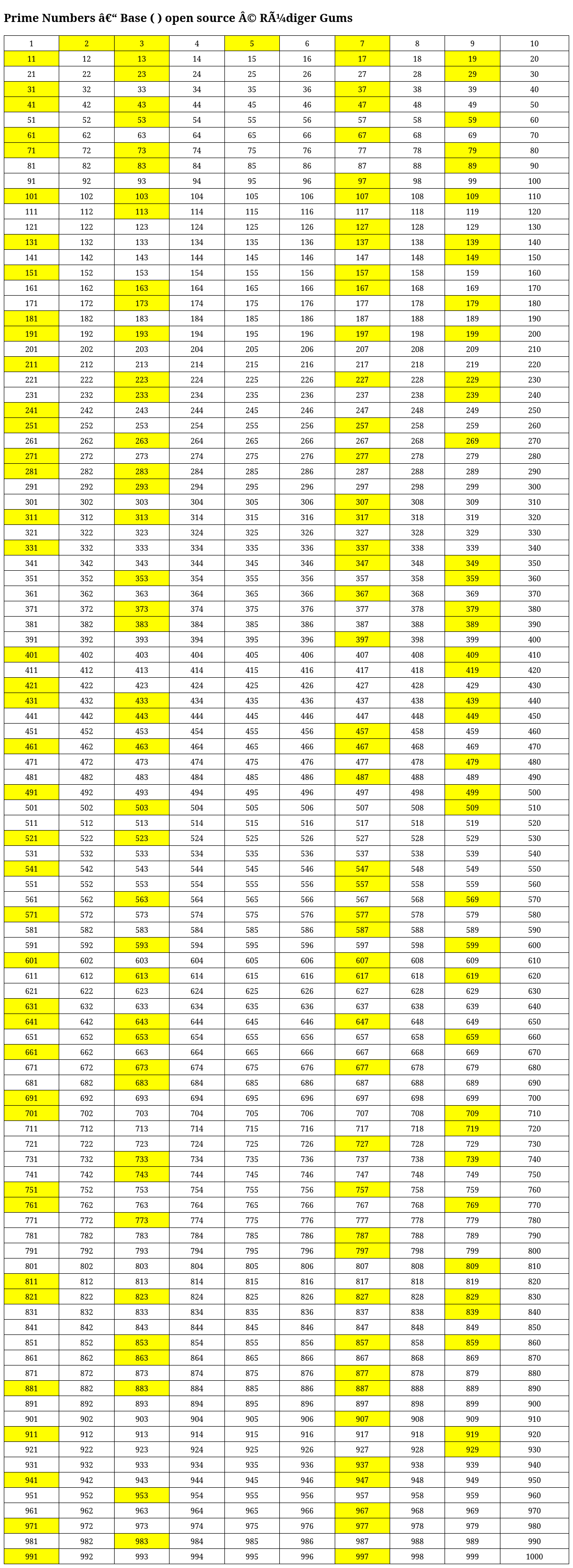
9b. Beispiele Primzahlen Tabellen Software 2

9c. Beispiele Primzahlen Tabellen Software 3

10a. RGUMS Prime Numbers Software 1 / markieren / kopieren

<!DOCTYPE html>

<html>

<head>

<title>Primzahlen-Tabelle (1–1000)</title>

<style>

table { border-collapse: collapse; width: 100%; }

th, td { border: 1px solid black; padding: 4px; text-align: center; }

.prime { background-color: yellow; }

</style>

</head>

<body>

<h2 id="headline"></h2>
<h2>Prime Numbers – Base ( ) open source © Rüdiger Gums
</h2>

</table>

// Funktion, um zu prüfen, ob eine Zahl eine Primzahl ist

function istPrimzahl(num) {

if (num <= 1) return false;

if (num === 2) return true;

if (num % 2 === 0) return false;

for (let i = 3; i <= Math.sqrt(num); i += 2) {

if (num % i === 0) return false;

}

return true;

}

// Tabelle mit 1000 Zeilen und 10 Spalten füllen

function fuelleTabelle() {

const table = document.getElementById("primzahlTabelle");

let zahl = 1;

for (let zeile = 0; zeile < 100; zeile++) {

const row = document.createElement("tr");

for (let spalte = 0; spalte < 10; spalte++) {

const cell = document.createElement("td");

cell.textContent = zahl;

// Primzahlen gelb markieren

if (istPrimzahl(zahl)) {

cell.classList.add("prime");

}

row.appendChild(cell);

zahl++;

}

table.appendChild(row);

}

// Tabelle beim Laden der Seite füllen

window.onload = fuelleTabelle;

</script>

</body>

</html>

10b. RGUMS Prime Numbers Software 2 / markieren / kopieren

<!DOCTYPE html>
<html lang="de">
<head>
<meta charset="UTF-8" />
<title>Primzahlen-Tabelle (Basis 16)</title>
<style>
table { border-collapse: collapse; width: 100%; font-family: monospace; }
td { border: 1px solid black; padding: 4px; text-align: center; }
.prime { background-color: yellow; }
</style>
</head>
<body>
<h2 id="headline"></h2>
<h2>Prime Numbers – Base ( ) open source © Rüdiger Gums
</h2>
<table id="primzahlTabelle"></table>
<script>
// ======= Einstellungen =======
const BASE = 16; // <-- 15 für Basis-15 (0-9,A-E) oder 16 für Hex (0-9,A-F)
const START = 1; // <-- 1 wie bisher; wenn du wirklich bei 0 starten willst: 0
const ROWS = 1000; // Anzahl Zeilen
// Spalten passend zur Basis (Basis-15 => 15 Spalten, Basis-16 => 16 Spalten)
const COLS = BASE;
// ============================
// Primzahltest (intern "normal" gerechnet – unabhängig von der Basis-Darstellung)
function istPrimzahl(num) {
if (num <= 1) return false;
if (num === 2) return true;
if (num % 2 === 0) return false;
for (let i = 3; i <= Math.sqrt(num); i += 2) {
if (num % i === 0) return false;
}
return true;
}
// Dezimalzahl -> Darstellung in Basis BASE (Buchstaben groß)
function toBaseN(num) {
return num.toString(BASE).toUpperCase();
}
function fuelleTabelle() {
document.getElementById("headline").textContent =
`Prime Numbers Base ${BASE} (Start: ${START})`;
const table = document.getElementById("primzahlTabelle");
let zahl = START;
for (let r = 0; r < ROWS; r++) {
const row = document.createElement("tr");
for (let c = 0; c < COLS; c++) {
const cell = document.createElement("td");
// Anzeige im gewünschten Zahlensystem
cell.textContent = toBaseN(zahl);
// Markierung echter Primzahlen (zahl ist die "Zahl an sich", nicht die Schreibweise)
if (istPrimzahl(zahl)) {
cell.classList.add("prime");
}
row.appendChild(cell);
zahl++;
}
table.appendChild(row);
}
}
window.onload = fuelleTabelle;
</script>
</body>
</html>

10c. RGUMS Prime Numbers Software 3 / markieren / kopieren

<!DOCTYPE html>

<head>

<title>Primzahlen-Tabelle – Basis 42</title>

<style>

table {

border-collapse: collapse;

width: 100%;

font-family: monospace;

font-size: 11px;

}

td {

border: 1px solid black;

padding: 3px;

text-align: center;

}

.prime {

background-color: yellow;

}

</style>

</head>

<body>

<h2>Prime Numbers – Base ( ) open source © Rüdiger Gums

</h2>

// =====================

const BASE = 42;

const START = 1;

const ROWS = 100; // 100 × 42 = 4200 Zahlen

const COLS = 42;

const DIGITS = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdef";

// =====================

function istPrimzahl(n) {

if (n <= 1) return false;

if (n === 2) return true;

if (n % 2 === 0) return false;

for (let i = 3; i <= Math.sqrt(n); i += 2) {

if (n % i === 0) return false;

}

return true;

}

function toBase42(n) {

if (n === 0) return "0";

let out = "";

let num = n;

while (num > 0) {

const r = num % BASE;

out = DIGITS[r] + out;

num = Math.floor(num / BASE);

}

return out;

}